Binary Search

What is Binary Search?

Binary search bu oralig'ini qayta-qayta ikkiga bo'lish orqali tartiblangan massivda qo'llaniladigan qidiruv algoritmi.Binary search g'oyasi massivning tartiblanganligi haqidagi ma'lumotdan foydalanish va vaqt murakkabligini O(logN)ga kamaytirishdir.

Agar massivdagi elementlar tartiblangan tartibda boʻlsa, biz ikkilik qidiruv (binary search)dan foydalanishimiz mumkin. Ikkilik qidiruv - bu massivdagi o'rta elementni qayta-qayta ko'rib chiqadi va biz izlayotgan element chapda yoki o'ngda bo'lishi kerakligini aniqlaydi. Har safar buni qilganimizda, biz izlashimiz kerak bo'lgan elementlar sonini ikki baravar kamaytiradi, bu ikkilik qidiruvni chiziqli qidiruvga qaraganda ancha tezroq qiladi!

Ikkilik qidiruvning salbiy tomoni shundaki, u faqat ma'lumotlar tartiblangan bo'lsa ishlaydi.

Agar biz faqat bitta qidiruvni amalga oshirishimiz kerak bo'lsa, chiziqli qidiruvni amalga oshirish tezroq bo'ladi, chunki chiziqli qidiruvga qaraganda saralash ko'proq vaqt oladi. Agar biz ko'p qidiruvlarni amalga oshirmoqchi bo'lsak, takroriy qidiruvlar uchun ikkilik qidiruvdan foydalanishimiz uchun birinchi navbatda ma'lumotlarni saralashga arziydi.

binary search

When to use Binary Search?

• Ma'lumotlar strukturasi tartiblangan bo'lganda

• Ma'lumotlar strukturasining istalgan elementiga kirish doimiy(O(1)) vaqtni olganda

Binary Search Algorithm:

Bu algoritmda

• mid - qidiruv maydonini ikkiga bo'lib o'rta indexni oling

image

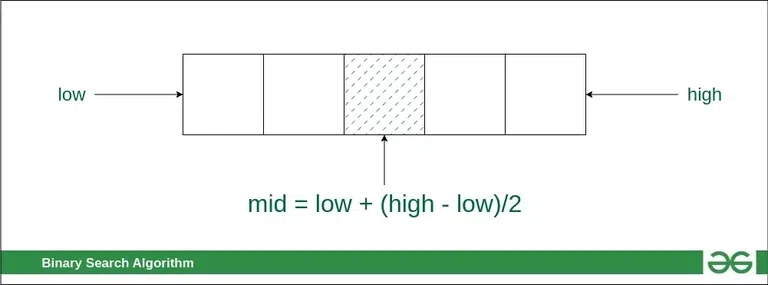
• Qidiruv maydonining o'rta elementini kalit bilan solishtiring.

• Agar kalit o'rta elementda topilsa, jarayon tugatiladi.

• Agar kalit o'rta elementda topilmasa, qaysi yarmi keyingi qidiruv maydoni sifatida ishlatilishini tanlang.

  • Agar kalit o'rta elementdan kichikroq bo'lsa, keyingi qidiruv uchun chap tomon ishlatiladi.

  • Agar kalit o'rta elementdan kattaroq bo'lsa, keyingi qidiruv uchun o'ng tomon ishlatiladi.

• Bu jarayon kalit topilmaguncha yoki umumiy qidiruv maydoni tugamaguncha davom ettiriladi.

How does Binary Search work?

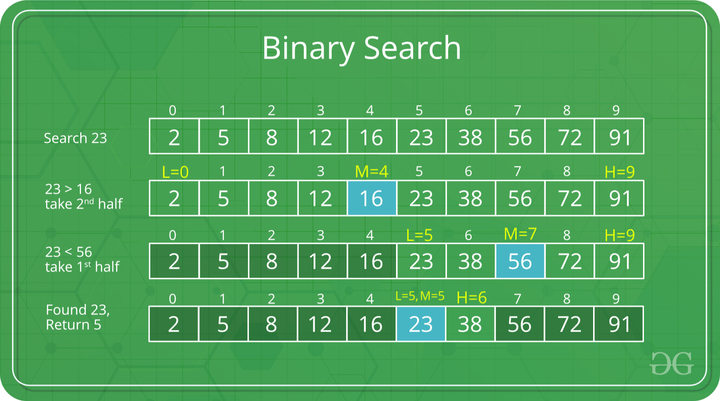
Binary Searchning ishlashini tushunish uchun quyidagi rasmni ko'rib chiqamiz: []arr = {2, 5, 8, 12, 16, 23, 38, 56, 72, 91} massivni va key = 23 ni ko'rib chiqamiz.

Step 1:

• O'rtadagi elementni toping va o'rta elementni kalit bilan solishtiring. Agar kalit o'rta elementdan kichik bo'lsa, chapga, agar u o'rtadan katta bo'lsa, qidiruv maydonini o'ngga o'tkazing.

• Kalit (ya'ni, 23) joriy o'rta elementdan (ya'ni, 16) kattaroqdir. Qidiruv maydoni o'ngga siljiydi. []arr = {23, 38, 56, 72, 91}

step 1

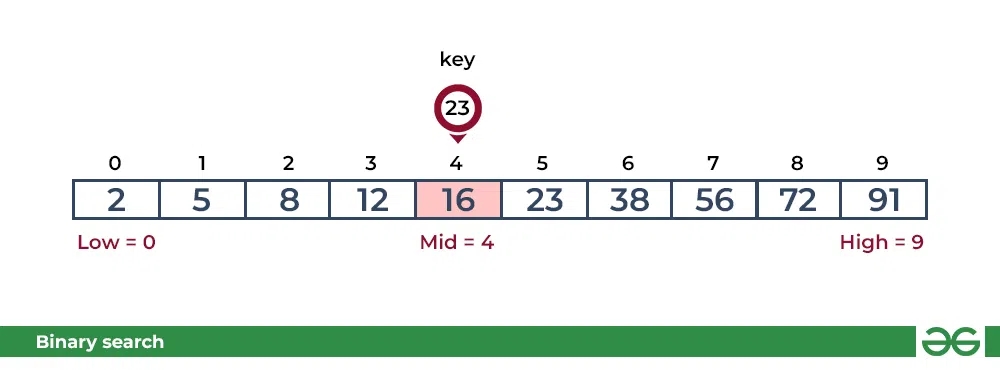
Step 2:

• Kalit joriy o'rta 56 dan kamroq. Qidiruv maydoni chapga siljiydi. []arr = {23, 38}

step 2

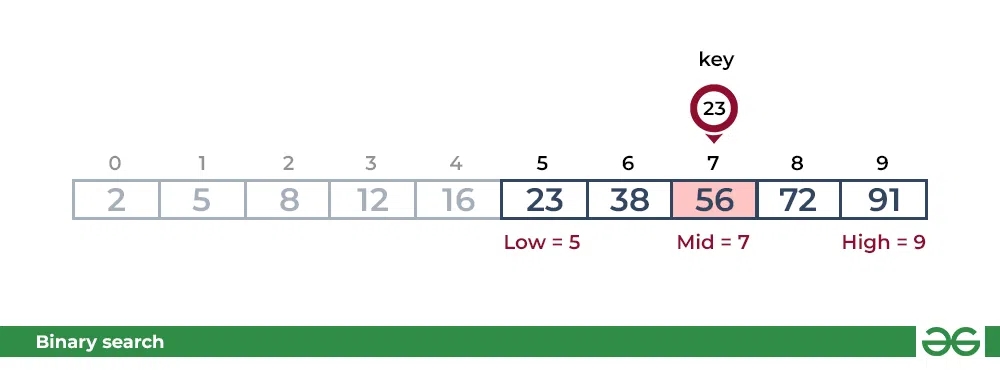
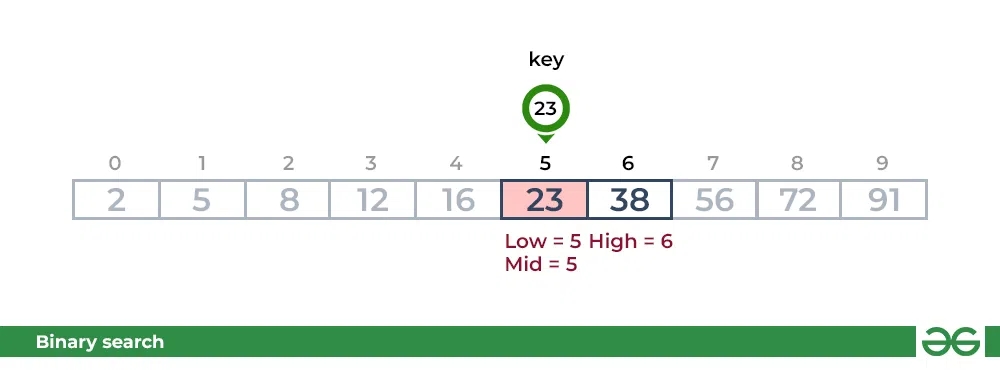
Step 3:

• Agar kalit o'rta elementning qiymatiga mos kelsa, element topiladi va qidiruvni to'xtatadi.

step 3

How to Implement Binary Search?

Binary Search algoritmi quyidagi ikki usulda amalga oshirilishi mumkin

• Iterative Binary Search Algorithm

• Recursive Binary Search Algorithm

Quyida yondashuvlar uchun psevdokodlar keltirilgan.

1. Iterative Binary Search Algorithm:

• Bu erda kalitni taqqoslash va qidiruv maydonini ikkiga bo'lish jarayonini davom ettirish uchun for tsiklidan foydalanamiz.

func binarySearch(arr []int, key int) int {
    low := 0
    high := len(arr) - 1
    for low <= high {
        mid := (low + high) / 2
        if arr[mid] == key {
            return mid
        } else if arr[mid] < key {
            low = mid + 1
        } else {
            high = mid - 1
        }
    }
    return -1
}

Kodni ishlatib ko'rish uchun playgrounddan foydalaning.

2. Recursive Binary Search Algorithm:

• Rekursiv funktsiya yarating va qidiruv maydonining o'rtasini kalit bilan solishtiring. Va natijaga asoslanib, kalit topilgan indeksni qaytaring yoki keyingi qidiruv maydoni uchun rekursiv funktsiyani chaqiring.

Rekursiv binary search algoritmini amalga oshirish:

// arr - tartiblangan massiv
// key - qidiriladigan element
// low - massivning boshlang'ich indeksi
// high - massivning oxirgi indeksi, ya'ni len(arr)-1
func binarySearch(arr []int, key, low, high int) int {
    
    // Massiv oxiriga yetib bo'lganligini tekshirish
    if low <= high {

        // Massivning o'rta elementini topish
        mid := low + (high-low)/2

        // Agar kalit o'rta elementga teng bo'lsa, o'rta elementni qaytarib chiqamiz
        if arr[mid] == key {
            return mid
        
        // Agar kalit o'rta elementdan kichik bo'lsa, qidiruv maydonini chap tomoniga siljiyamiz, ya'ni, high = mid-1
        } else if arr[mid] > key {
            return binarySearch(arr, key, low, mid-1)

        // Agar kalit o'rta elementdan katta bo'lsa, qidiruv maydonini o'ng tomoniga siljiyamiz, ya'ni, low = mid+1
        } else {
            return binarySearch(arr, key, mid+1, high)
        }
    }

    // Agar kalit topilmagan bo'lsa, -1 qaytarib chiqamiz
    return -1
}

Kodni ishlatib ko'rish uchun playgrounddan foydalaning.

Complexity Analysis of Binary Search:

• Time Complexity O(logN), bu yerda N - massiv uzunligi.

  • Best Case: O(logN)

  • Average Case: O(logN)

  • Worst Case: O(logN)

• Space Complexity: O(1), agar rekursiv binary search implementi ishlatilsa, O(logN) bo'ladi.

Advantages of Binary Search:

• Binary Search Linear Searchga qaraganda tezroq, ayniqsa katta massivlar uchun.

• Binary Search Interpolatsiyali qidiruv yoki eksponensial qidiruv kabi vaqt murakkabligi o'xshash boshqa qidiruv algoritmlariga qaraganda samaraliroq.

• Binary Search tashqi xotirada, masalan, qattiq diskda yoki cloudda saqlanadigan katta ma'lumotlar to'plamini qidirish uchun juda mos keladi.

Disadvantage of Binary Search:

• Massiv tartiblangan bo'lishi kerak.

• Binary Search izlanayotgan ma'lumotlar strukturasi qo'shni xotira joylarida saqlanishini talab qiladi.

• Binary Search massivning elementlarini solishtirishni talab qiladi, ya'ni ularni tartiblash imkoniyati bo'lishi kerak.

Source: GeeksforGeeks