104. Maximum Depth of Binary Tree

🟩 Easy

Given the root of a binary tree, return its maximum depth.

A binary tree's maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

Example 1

tree

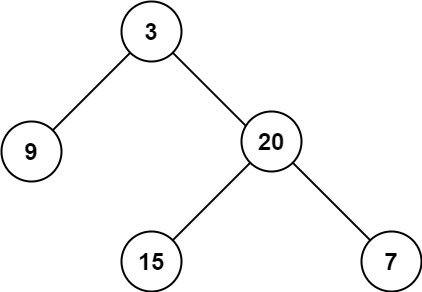
Input: root = [3,9,20,null,null,15,7] Output: 3

Example 2

Input: root = [1,null,2] Output: 2

Constraints

• The number of nodes in the tree is in the range [0, 10^4].

• -100 <= Node.val <= 100

Solution

My Solution

func maxDepth(root *TreeNode) int {
    if root == nil {
        return 0
    }

    if root.Left == nil && root.Right == nil {
        return 1
    }

    if root.Left == nil {
        return maxDepth(root.Right) + 1
    }

    if root.Right == nil {
        return maxDepth(root.Left) + 1
    }

    return max(maxDepth(root.Right), maxDepth(root.Left))+1
}

Optimal Solution (Concise DFS)

func maxDepth(root *TreeNode) int {
    if root == nil {
        return 0
    }
    return 1 + max(maxDepth(root.Left), maxDepth(root.Right))
}

Alternative Solution (Iterative BFS)

func maxDepth(root *TreeNode) int {
    if root == nil {
        return 0
    }
    
    depth := 0
    queue := []*TreeNode{root}
    
    for len(queue) > 0 {
        levelSize := len(queue)
        depth++
        
        // Process all nodes at current level
        for i := 0; i < levelSize; i++ {
            node := queue[0]
            queue = queue[1:]
            
            if node.Left != nil {
                queue = append(queue, node.Left)
            }
            if node.Right != nil {
                queue = append(queue, node.Right)
            }
        }
    }
    
    return depth
}

Approach Analysis

This problem can be solved in multiple ways:

1. Your Solution (Explicit DFS):

   • Handles each case separately

   • Very clear and readable

   • Explicitly checks for leaf and single-child cases

   • Good for understanding the problem

2. Optimal DFS Solution:

   • More concise implementation

   • Implicitly handles all cases

   • Same time/space complexity

   • Relies on max function elegantly

3. BFS Alternative:

   • Level-order traversal

   • Counts depth level by level

   • Uses queue data structure

   • Good for level-based operations

Complexity Analysis

Time Complexity: O(n)

• All solutions visit each node exactly once

• Constant work per node

• n is total number of nodes

Space Complexity

• DFS Solutions: O(h)

  • h is height of tree

  • Recursive call stack

  • Best: O(log n) for balanced

  • Worst: O(n) for skewed

• BFS Solution: O(w)

  • w is maximum width of tree

  • Queue size at widest level

  • Best: O(1) for skewed

  • Worst: O(n/2) for perfect binary tree

Why Different Approaches Work

• Your Solution:

  • Explicit case handling

  • Clear logic flow

  • Good for debugging

  • Easy to modify for variations

• Optimal DFS:

  • Mathematical elegance

  • Recursive subproblem

  • Minimal code

  • Same efficiency

• BFS Approach:

  • Natural level counting

  • No recursion needed

  • Easy to modify for related problems

  • Good for level-specific tasks

Common Patterns & Applications

• Similar Problems:

  • Minimum Depth of Binary Tree

  • Balanced Binary Tree

  • Diameter of Binary Tree

• Tree Traversal Patterns:

  • DFS: Pre/In/Post order

  • BFS: Level order

  • Each has its use cases

• When to Use Each:

  • DFS: Path-related problems

  • BFS: Level-related problems

  • Your solution: When clarity is priority

  • Optimal: When conciseness matters

result

Leetcode: link