637. Average of Levels in Binary Tree
Easy
Given the root of a binary tree, return the average value of the nodes on each level in the form of an array. Answers within 10^-5 of the actual answer will be accepted.
Example 1
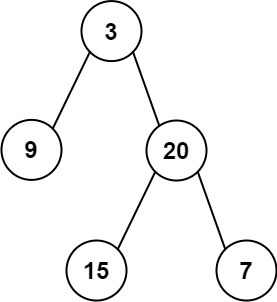
Input: root = [3,9,20,null,null,15,7] Output: [3.00000,14.50000,11.00000] Explanation: The average value of nodes on level 0 is 3, on level 1 is 14.5, and on level 2 is 11. Hence return [3, 14.5, 11].
Example 2
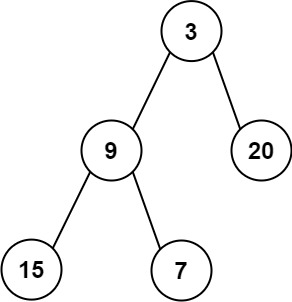
Input: root = [3,9,20,15,7] Output: [3.00000,14.50000,11.00000]
Constraints
The number of nodes in the tree is in the range
[1, 10^4].-2^31 <= Node.val <= 2^31 - 1
Solution
My Solution
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func averageOfLevels(root *TreeNode) []float64 {
resp := []float64{}
queue := []*TreeNode{root}
for len(queue) != 0 {
size := len(queue)
level := 0
for i:=0; i < size; i++ {
level += queue[i].Val
if queue[i].Left != nil {
queue = append(queue, queue[i].Left)
}
if queue[i].Right != nil {
queue = append(queue, queue[i].Right)
}
}
queue = queue[size:]
resp = append(resp, float64(level)/float64(size))
}
return resp
}Optimal Solution
The optimal solution uses level-order traversal (BFS) with two key improvements:
Using
int64to handle potential integer overflowPre-allocating the result slice for better performance
Efficient queue management with slice operations
func averageOfLevels(root *TreeNode) []float64 {
if root == nil {
return nil
}
// Pre-allocate result slice (optimization)
result := make([]float64, 0, 10000) // max nodes = 10^4
// Initialize queue with root
queue := []*TreeNode{root}
for len(queue) > 0 {
levelSize := len(queue)
levelSum := int64(0) // Use int64 to prevent overflow
// Process current level
for i := 0; i < levelSize; i++ {
node := queue[0]
queue = queue[1:] // More efficient queue management
levelSum += int64(node.Val)
// Add children to queue
if node.Left != nil {
queue = append(queue, node.Left)
}
if node.Right != nil {
queue = append(queue, node.Right)
}
}
// Calculate and store average
avg := float64(levelSum) / float64(levelSize)
result = append(result, avg)
}
return result
}Approach Analysis
The solution employs two main techniques:
Level-Order Traversal (BFS):
Uses queue data structure
Processes nodes level by level
Maintains level boundaries
Ensures correct level averages
Efficient Memory Management:
Pre-allocated result slice
Optimized queue operations
Integer overflow prevention
Proper type conversions
Visualization of Both Approaches
Example Tree:
3
/ \
9 20
/ \
15 7
BFS Traversal Steps:
Level 0: [3]
Queue: [3]
Sum: 3
Average: 3.0
Level 1: [9, 20]
Queue: [9, 20]
Sum: 29
Average: 14.5
Level 2: [15, 7]
Queue: [15, 7]
Sum: 22
Average: 11.0
Final Result: [3.0, 14.5, 11.0]Complexity Analysis
Time Complexity:
O(n) - visit each node exactly once
O(1) - queue operations (append/remove)
O(1) - average calculation per level
Total: O(n) where n is number of nodes
Space Complexity:
O(w) - queue size (w = max width of tree)
O(h) - result array (h = height of tree)
Total: O(w) where w is maximum width
Optimizations:
Pre-allocated result slice
int64 for overflow prevention
Efficient queue management
Early nil check
Why Solution Works
BFS Properties:
Natural level-by-level traversal
Maintains level boundaries
Complete level processing
Correct order guarantee
Memory Management:
Efficient slice operations
No extra data structures
Minimal memory overhead
Prevents integer overflow
Average Calculation:
Accurate level tracking
Proper type handling
Precision maintenance
Overflow prevention
When to Use
This approach is ideal when:
Need level-by-level tree processing
Require level-based calculations
Memory can handle tree width
Order within levels doesn't matter
Common applications:
Level-order tree traversal
Level statistics calculation
Tree visualization
Level-based tree operations
Common Patterns & Applications
BFS Pattern:
Queue-based traversal
Level-by-level processing
Width-first exploration
Level boundary tracking
Tree Level Processing:
Level statistics
Level modifications
Level grouping
Level comparisons
Average Calculations:
Numeric overflow handling
Floating-point precision
Group-based statistics
Level-based metrics
Interview Tips
Initial Clarification:
Confirm if we need to handle empty tree
Ask about precision requirements for averages
Clarify if the order of nodes within levels matters
Discuss memory constraints for large trees
Solution Walkthrough:
Start with BFS approach explanation
Mention queue usage for level tracking
Explain why BFS is better than DFS here
Discuss integer overflow prevention
Code Implementation Strategy:
Begin with basic queue structure
Add level size tracking
Implement sum calculation with overflow prevention
Handle edge cases last
Optimization Discussion:
Pre-allocate slices for better performance
Use int64 for sum to prevent overflow
Efficient queue management with slice operations
Early termination for nil root
Common Pitfalls to Avoid:
Integer overflow with large numbers
Not tracking level boundaries correctly
Inefficient queue operations
Missing edge cases
Follow-up Questions:
Q: "How would you handle a very wide tree?" A: Use level-by-level processing to limit memory usage
Q: "Can we solve this using DFS?" A: Yes, using a map to track level sums and counts
Q: "How to optimize memory usage?" A: Process nodes level by level, reuse queue space
Q: "What if we need exact decimal precision?" A: Use big.Float or similar for precise calculations
Edge Cases to Test:
Empty tree: return empty slice
Single node: return [node.Val]
Complete binary tree: maximum width
Skewed tree: minimal width
Large values: potential overflow
Code Quality Points:
Clear variable names (levelSize, levelSum)
Proper type conversions
Early return for nil
Clean queue management
Consistent error handling
Alternative Approaches:
DFS with level tracking
Iterative vs recursive
Array-based complete tree
Morris traversal variation
Performance Analysis:
Time: O(n) - visit each node once
Space: O(w) - w is max tree width
Memory-time tradeoffs
Optimization possibilities
Leetcode: link
Last updated
Was this helpful?