11. Container With Most Water

🟧 Medium

You are given an integer array height of length n. There are n vertical lines drawn such that the two endpoints of the i^th line are (i, 0) and (i, height[i]).

Find two lines that together with the x-axis form a container, such that the container contains the most water.

Return the maximum amount of water a container can store.

Notice that you may not slant the container.

Example 1

image

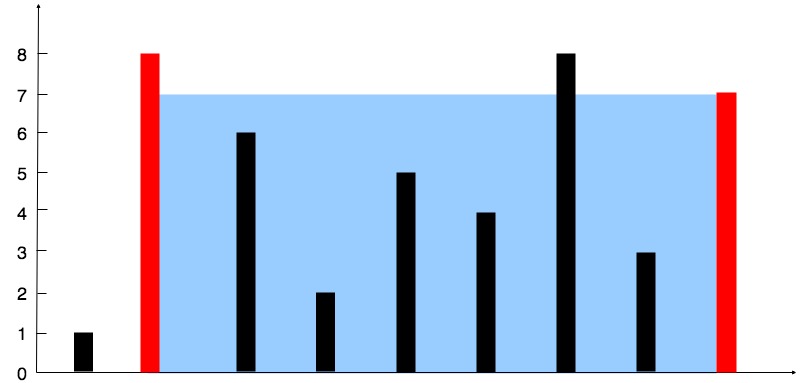
Input: height = [1,8,6,2,5,4,8,3,7] Output: 49 Explanation: The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.

Example 2

Input: height = [1,1] Output: 1

Constraints

• n == height.length

• 2 <= n <= 10^5

• 0 <= height[i] <= 10^4

Solution

My Solution

func maxArea(h []int) int {
    area := 0

    l, r :=0, len(h)-1
    for l <= r {
        area = max(area,(r-l)*min(h[l],h[r]))
        if h[l] < h[r] {
            l++
        } else {
            r--
        }
    }

    return area
}

Optimal Solution (Two Pointer Approach)

func maxArea(height []int) int {
    maxArea, left, right := 0, 0, len(height)-1
    
    for left < right {
        width := right - left
        h := min(height[left], height[right])
        maxArea = max(maxArea, width*h)
        
        if height[left] < height[right] {
            left++
        } else {
            right--
        }
    }
    
    return maxArea
}

Approach

The Two Pointer technique is used to solve this problem efficiently:

1. Initialize two pointers:

   • Left pointer at the start (index 0)

   • Right pointer at the end (index n-1)

2. Calculate area at each step:

   • Width = right - left (distance between lines)

   • Height = min(height[left], height[right])

   • Current area = width * height

3. Update maximum area if current area is larger

4. Move pointers strategically:

   • If height[left] < height[right], move left pointer right

   • If height[right] <= height[left], move right pointer left

   • This ensures we always explore the possibility of finding a larger area

Complexity Analysis

Time Complexity: O(n)

• We traverse the array exactly once

• Each element is visited at most once by either left or right pointer

• All operations inside the loop (min, max) are O(1)

Space Complexity: O(1)

• We only use three variables regardless of input size:

  • maxArea - to store the maximum area

  • left - left pointer

  • right - right pointer

Why it works

• Uses two pointers to track potential container boundaries

• Always moves the pointer with smaller height inward

• Area is limited by the smaller height, so moving the taller pointer would never give a better result

• Efficiently finds the maximum area by considering all possible optimal container configurations

result

Leetcode: link